letter to nature
Cover:
A Doubling of the Sun's Coronal Magnetic Field during the Last 100 Years
M. Lockwood, R. Stamper, and M.N. Wild
World Data Centre C-1 for STP, Rutherford Appleton Laboratory, Chilton, England, UK
NATURE Vol. 399, 3 June 1999. Pages 437-439
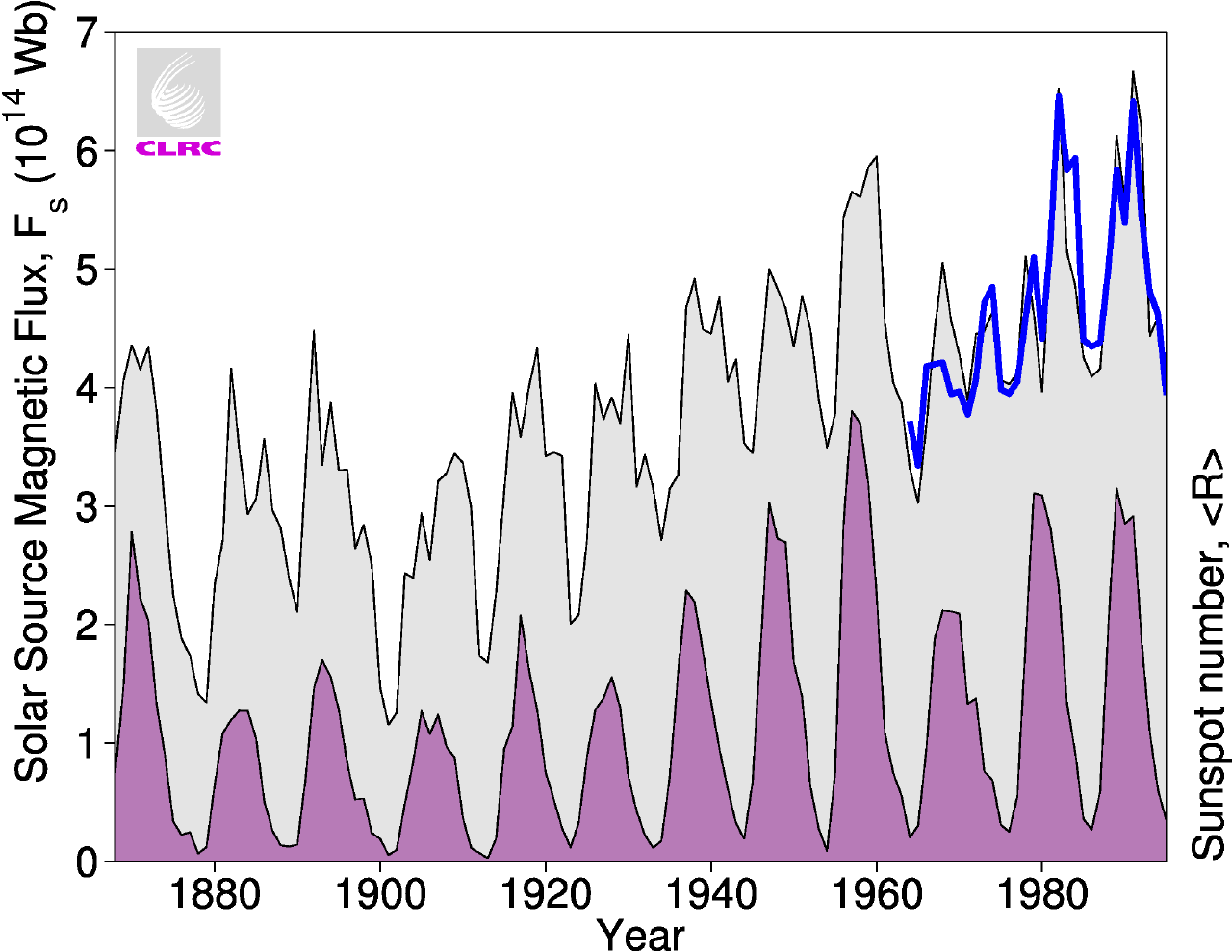
The total solar magnetic flux emanating through the coronal source sphere8, , derived from the geomagnetic aa data for 1868-1996 (black line bounding grey shading) and the values from the interplanetary observations for 1964-1996 (blue line). The variation of the annual means of the sunspot number is shown by the area shaded purple. The magnetic flux in the solar corona has risen by 40% since 1964 and by a factor of 2.3 since 1901.
NATURE Vol. 399, 3 June 1999. Pages 437-439
A Doubling of the Sun's Coronal Magnetic Field during the Last 100 Years
M. Lockwood, R. Stamper, and M.N. Wild
World Data Centre C-1 for STP, Rutherford Appleton Laboratory, Chilton, England, UK
The solar wind, because it is an extended ionized gas of very high electrical conductivity, drags some magnetic flux out of the Sun, thereby filling the heliosphere with the weak interplanetary magnetic field 7, 24. Magnetic reconnection - the merging of oppositely-directed magnetic fields such that they become connected to each other - between the interplanetary field and the Earth's magnetic field, allows energy from the solar wind to enter the near-Earth environment. The Sun's properties, such as its luminosity, are related to its magnetic field, though the connections are as yet not well understood 15, 16. Moreover, changes in the heliospheric magnetic field have been linked with changes in total cloud cover over the Earth, which may influence global climate change 17. Here we report that the measurements of the near-Earth interplanetary magnetic field reveal that the total magnetic field leaving the sun has risen by a factor 1.4 since 1964. Using surrogate interplanetary measurements, we find that the rise since 1901 is by a factor of 2.3. This change may be related to chaotic changes in the dynamo that generates the solar magnetic field. We do not yet know quantitatively how such changes will influence the global environment.
The aa index has been compiled from the range of variations in the geomagnetic field during three-hourly periods, recorded since 1868 by pairs of near-antipodal magnetometers in England and Australia1. Figure 1 demonstrates that the annual means <aa> show a marked variation with the sunspot cycle, but have also drifted upward throughout most of this century. These changes are almost entirely due to variations in near-Earth interplanetary space2. Several attempts have been made to use the aa data to deduce the interplanetary and solar conditions before the space age3, 4, 5. The success of these extrapolations depends critically on the quality of the correlation found between aa and the combination of the interplanetary parameters (the empirical "coupling function" 6 ) used to quantify the controlling influence of the solar wind and the interplanetary magnetic field (IMF). Recently, an unprecedentedly high and significant correlation coefficient of 0.97 has been obtained 2.
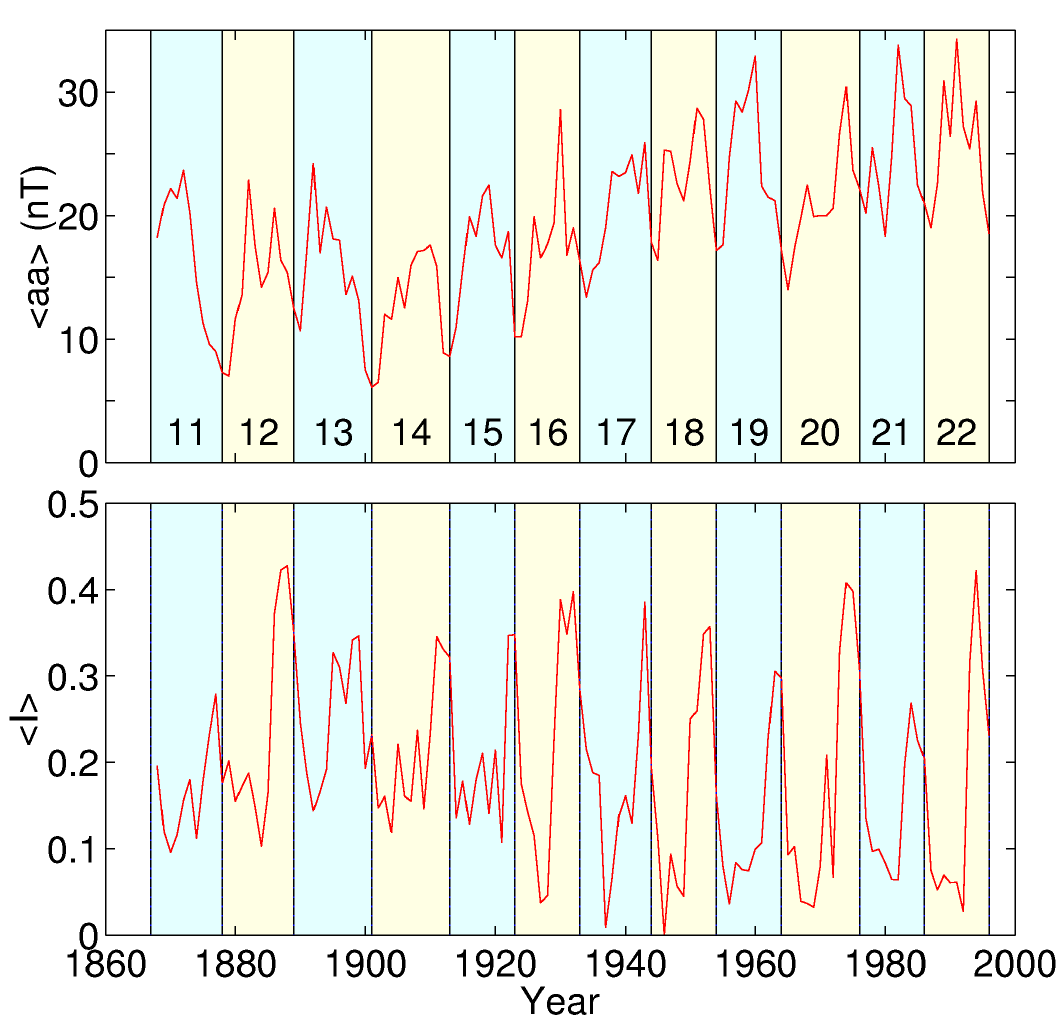
Figure 1. Annual means of (a) the aa geomagnetic activity index , <aa> and (b) Sargent's recurrence index, <I> (defined for the jth 27-day Carrington rotation period as , where c is the correlation coefficient between two consecutive 27-day intervals of twelve-hourly aa values22, 9 ). The data are for 1868-1996, covering sunspot cycles 11-22: the solar cycles, commencing at sunspot minimum, are shaded alternately yellow and blue. Non-recurrent increases in aa are caused by solar disturbances, such as coronal mass ejections, hitting the Earth's magnetosphere. This occurs more frequently at sunspot maximum25. In the declining phase of each sunspot cycle, <aa> is high because Earth intersects long-lived, fast solar wind streams9. These emanate from coronal holes that have expanded to low heliospheric latitudes21 and rotate with the equatorial photosphere every 25 days. During this time, the Earth moves along its orbit, such that it intersects the same stream every 27 days, giving recurrent geomagnetic storms and high <I>.9 Several long-term trends are apparent: for all phases of the solar cycle, <aa> increased gradually between 1900 and about 1955, before decreasing and then rising again during 1964-1996. Similar trends can be seen in the sunspot number maxima (see Figure 3). The recurrent element of geomagnetic activity at sunspot maximum, as quantified by <I>, fell during the early part of the century, but the sunspot minimum/declining phase peaks in <I> remained high with a tendency for greater values during even-numbered sunspot cycles23.
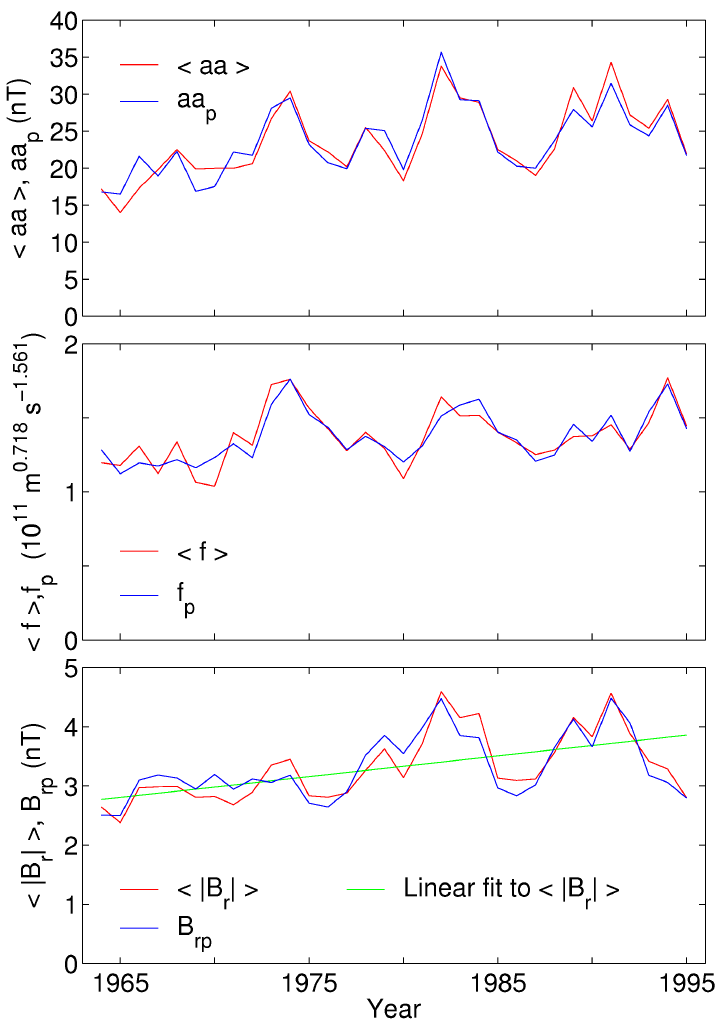
The method section describes a novel procedure by which we derive information on the magnetic field in the solar atmosphere (corona) from the <aa> data. Fs is the magnetic flux that threads a roughly spherical "source" surface in the corona where the sun's field becomes purely radial: it quantifies the amount of flux leaving the sun and entering the heliosphere. The method employs three correlations of extremely high significance for the period 1964-1996. Figure 2 shows the good agreement between observed yearly averages and their best-fit predicted values, derived using these correlations. Figure 2a shows the observed and predicted annual means of aa (<aa> and aap, respectively), 2b is the same for the function f (see method section), and 2c is for the magnitude of the radial component of the IMF |Br|.
The orientation of the IMF in annual averages is as predicted by Parker Spiral theory2, 7. This theory also predicts that the rise in the magnitude of the mean radial component, seen in Figure 2c, reflects a corresponding change in the coronal source field Bo (equation 5). A least-squares linear fit to <|Br|> for 1964-1996 (the green line in 2c) yields a percent change (defined as 100 times the change, divided by the initial value) of 41% (± 13%). In other words, there has been a rise by a factor of 1.41 over the last three solar cycles. This rise is present, but not commented on, in previously published coronal source field estimates, modelled from the measured solar photospheric field8. Cosmic rays are shielded from Earth by both the IMF and the solar wind flow and the observed decay in cosmic ray fluxes (by 3.7% since 1964) 2, 9 is, at least qualitatively, consistent with the rise in the IMF.
The results of the extrapolation to before 1964 are shown in Figure 3. The values of Fs derived from the aa data are shown in grey and compare well with those from the observed annual means of the IMF radial component <|Br|> for 1964-1996 (thick blue line). The coronal source flux rises and falls in each solar cycle, lagging only slightly behind the sunspot numbers R, shown in purple. The main differences between Fs and <aa> arise because the effects of the recurrent fast solar wind streams (in the declining phase of each cycle9) have effectively been removed by our procedure. For data at all phases of the solar cycle, Fs has a correlation coefficient of 0.75 with the simultaneous R (giving a significance level of effectively 100%). To eliminate the solar cycle variations, we have studied the 11-year running means and those for Fs and R vary in a very similar way. In 1901, the 11-year running mean of Fs was a minimum of 2.308 ´ 1014 Wb, but rose to a peak value of 5.325 ´ 1014 Wb in 1992. Thus in the intervening 91 years (covering roughly 8.5 sunspot cycles) there was a rise in the average solar source flux of 131% (i.e. a rise by a factor of 2.31).

These changes in the solar magnetic field should be seen in the context of longer-term changes in the sun, as inferred from historical sunspot and auroral observations10 and from the terrestrial abundances of isotopes such as 14C and 10Be (produced by cosmic ray bombardment and deposited and stored, for example, in the polar icecaps)11, 12. The isotope data show solar activity can largely disappear for periods of 50-100 years, such as the Maunder minimum (1650-1700), although there is evidence that a weak and cyclic magnetic field still emerged from the sun12. By comparing the phase of the 88-year oscillation prior to and after the Maunder minimum, it has been inferred that the dynamo generating the solar field may be chaotic rather than quasi-periodic13: such behaviour may be relevant to the sudden changes in Fs around 1900 and 1960. Recent studies have linked changes in solar activity and aa with terrestrial climate change14, 15, 16, 17. The variation found here stresses the importance of understanding the connections between the sun's output and its magnetic field15, 16 and between terrestrial global cloud cover, cosmic ray fluxes and the heliospheric field17.
Method
We employ the optimum energy coupling function between the solar wind and the Earth's magnetosphere derived by Stamper et al.2 using the dimensional analysis proposed by Vasyliunas et al.18. The solar wind kinetic energy density dominates over the energy densities of both thermal motions and the IMF. This is incident on the geomagnetic field, which presents a roughly circular cross section to the flow. A fraction of the incident energy is extracted, the power transferred to the magnetosphere being2 :
where is the mean ion mass, the concentration and the speed of the solar wind. is the IMF magnitude, is the IMF orientation "clock angle" 19 , is the magnetic moment of the Earth (taken from the IGRF model20 ), and are constants and is the best-fit prediction of . From annual means for 1964-1996, the best-fit "coupling exponent" α is found to be 0.386,2 and is obtained from a linear regression fit of <aa> against . The largest factor contributing to the rise in <aa> since 1964 is an upward drift in , with significant rises in and ; however the mean has grown somewhat less favourable for increasing <aa>.2 The dependence is sufficient to allow derivation of from <aa>. In order to separate the effect of from that of the other interplanetary variables, we define a parameter :
the variation of which is dominated by that in the solar wind speed . The annual mean of rises in the declining phase of solar cycles9 because the Earth repeatedly intersects fast solar wind streams from low-latitude extensions of coronal holes21. These occur every 27 days and so also raise the geomagnetic recurrence index, (see Figure 1)22. Hence we expect and to increase together in the declining phase of the sunspot cycle. However, can remain high at sunspot minimum (whereas is lower) because aa values are low and relatively constant23. Hence we adopted a relationship for a predicted of the form:
where the exponents β and λ give the optimum correlation and the constants and are then found from a linear regression fit. The primary justification for the use of (3) is that it yields a correlation which is comparable (in magnitude and significance) to the other two shown in Figure 2. Note that reproduces both the drift and 22-year cycle in . From (1)-(3) we can obtain a formula for estimating from the index data series:
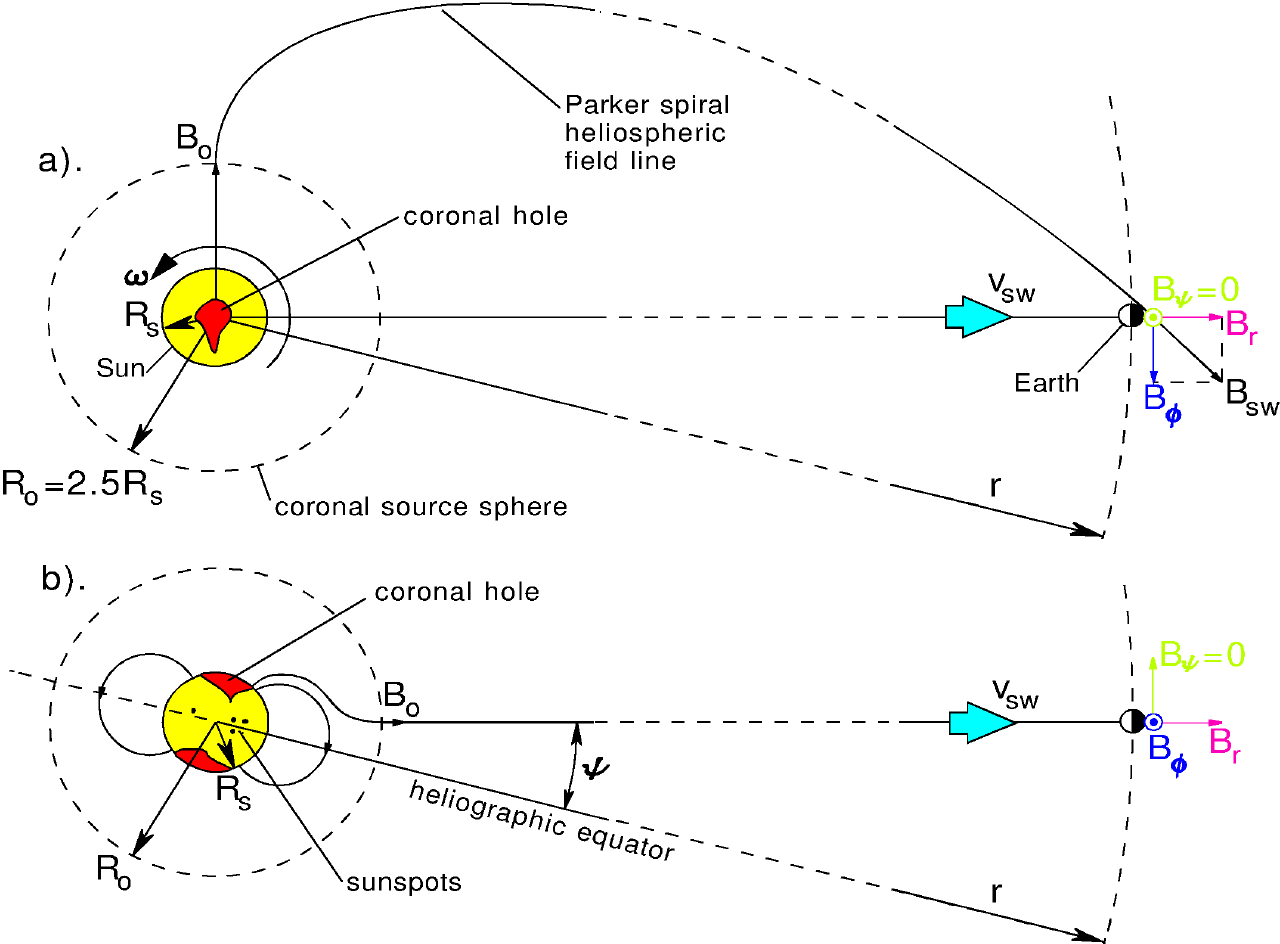
Parker spiral theory successfully predicts the radial and latitudinal variations of the annual means of the heliospheric field2,7 :
where is the coronal source field at from the centre of the sun8, ω is the equatorial angular solar rotation velocity and ψ is the heliographic latitude (see Figure 4). In annual means, the modulus of the out-of-ecliptic IMF component is well correlated with and the mean is close to zero. The "garden hose angle" g of the IMF in the ecliptic plane (equal to tan-1Bf /Br ) remains close to 45° and so the radial heliospheric field component Br is roughly proportional to Bsw, i.e. Br = sB Bsw (Figure 2c). In addition, recent observations by the Ulysses satellite have shown that latitudinal variations in the heliospheric field are small (Br is independent of y )24. This result has been used to derive the coronal source field Bo from photospheric field measurements and good agreement found with observations of Br near Earth at all phases of the solar cycle8. The total magnetic flux of the sun that threads the source surface (radius Ro), Fs, is:
where r = 1AU for observations near Earth 8. The factor of one half arises because half the field threading the source surface is inward, the other half outward. We can compute the solar flux from the aa data using equations (4) and (6).
In order to extrapolate to before 1964, we assume that all three correlations (derived from the data for after 1964) were valid at all times since 1868. Specifically, we assume that the empirical functions and behave as they did after 1964. We also assume that the empirical coupling exponent a and the mean mass of the solar wind are constant, that Parker spiral theory applied and that latitudinal variations in the heliospheric field were small then as now.
Acknowledgements. The data used are stored and made available via World Data Centre, C1 for STP at RAL, which is funded by the UK Particle Physics and Astronomy Research Council and, until 1 April 1999, by the National Radio Propagation Programme of the UK Radiocommunications Agency. We also thank the many scientists who have contributed data to the WDC.
References
1 Mayaud, P.N., The aa indices: a 100-year series characterising the magnetic activity, J. Geophys. Res., 72, 6870-6874 (1972).
2 Stamper, R., M. Lockwood, M.N. Wild, and T.D.G. Clark, Solar Causes of the Long-Term Increase in Geomagnetic Activity, J. Geophys Res., in press (1999).
3 Russell, C.T., On the possibility of deducing interplanetary and solar parameters from geomagnetic records, Solar Physics, 42, 259-269 (1975).
4 Gringauz, K.I., Average characteristics of the solar wind and its variation during the solar cycle, in "Solar Wind 4", Report MPAE-W-100-81-31, edited by H. Rosenbauer, MPI fuer Aeronomie, Lindau, Germany (1981)
5 Feynman, J., and N.U. Crooker, The solar wind at the turn of the century, Nature, 275, 626-627 (1978)
6 Baker, D. Statistical analyses in the study of Solar Wind-Magnetosphere coupling, in "Solar Wind-Magnetosphere Coupling" edited by Y. Kamide and J.A. Slavin, pp17-38, Terra Scientific, Tokyo (1986)
7 Gazis, P.R., Solar cycle variation of the heliosphere, Rev. Geophys., 34, 379-402 (1996)
8 Wang, Y.-M. and N.R. Sheeley, Jr., Solar implications of Ulysses interplanetary field measurements, Astrophys. J., 447, L143-L146 (1995)
9 Cliver, E.W., V. Boriakoff, and K.H. Bounar, The 22-year cycle of geomagnetic activity, J. Geophys. Res., 101, 27091-27109 (1996)
10 Silverman, S.W., Secular variation of the aurora for the past 500 years, Rev. Geophys., 30, 333-351 (1992)
11 Sonnet, C.P., Long-period solar-terrestrial variability, in U.S. National Report to IUGG, 1987-1990, Suppl. to Rev. Geophys., 909-914 (1991)
12 Beer, J., S. Tobias, and N. Weiss, An active sun throughout the Maunder minimum, Solar Physics, 181, 237-249 (1998)
13 Feynman, J. and S.B. Gabriel, Period and phase of the 88-year solar cycle and the Mainder minimum: evidence for the chaotic sun, Solar Physics, 127, 393-403 (1990)
14 Cliver, E.W., V. Boriakoff, and J, Feynman, Solar Variability and climate change: geomagnetic aa index and global surface temperature, Geophys. Res. Lett., 25, 1035-1038, 1998
15 Willson, R.C., Total solar irradiance trend during cycles 21 and 22, Science, 277, 1963-1965 (1997)
16 Lean, J., J. Beer, and R. Bradley, Reconstruction of solar irradiance since 1610: implications for climate change, Geophys. Res. Lett., 22, 3195-3198, 1995
17 Svensmark, H., and E. Friis-Christensen, Variation of cosmic ray flux and global cloud coverage � a missing link in solar-climate relationships, J. atmos. Sol. Terr. Phys., 59, 1225-1232 (1997)
18 Vasyliunas, V.M., J.R. Kan, G.L. Siscoe, and S.-I. Akasofu, Scaling relations governing magnetospheric energy transfer, Planet Space Sci., 30, 359-365 (1982)
19 Scurry L., and C.T. Russell, Proxy studies of energy transfer to the magnetosphere, J. Geophys. Res., 96, 9541-9548 (1991)
20 Merrill, McElhinny and McFadden, The magnetic Field of the Earth, Academic press, p. 34, (1996)
21 Wang, Y.-M., S.H. Hawley, and N.R. Sheeley, Jr.,. The magnetic nature of coronal holes, Science, 271, 464-469 (1996)
22 Sargent, H.H. III, The 27-day recurrence index, , in "Solar Wind-Magnetosphere Coupling" edited by Y. Kamide and J.A. Slavin, pp143-148, Terra Scientific, Tokyo (1986)
23 Hapgood, M.A., A double solar-cycle variation in the 27-day recurrence of geomagnetic activity, Ann Geophys., 11, 248 (1993)
24 Balogh, A., E.J. Smith, B.T. Tsurutani, D.J. Southwood, R.J. Forsyth and T.S. Horbury, The heliospheric field over the south polar region of the sun, Science, 268, 1007-1010 (1995)
25 Webb, D.F and R.A. Howard, The solar cycle variation of coronal mass ejections and solar wind mass flux, J. Geophys. Res., 99, 4201 (1994)