In press with Geophys Res. Lett.
May 1999
Long-term drift of the coronal source magnetic flux and the total solar irradiance
M. Lockwood,1 and R. Stamper
World Data Centre C1, Rutherford Appleton Laboratory, Chilton, Oxfordshire, UK.
Abstract. We test the method of Lockwood et al. [1999] for deriving the coronal source flux from the geomagnetic aa index and show it to be accurate to within 12% for annual means and 4.5% for averages over a sunspot cycle. Using data from four solar constant monitors during 1981-1995, we find a linear relationship between this magnetic flux and the total solar irradiance. From this correlation, we show that the 131% rise in the mean coronal source field over the interval 1901-1995 corresponds to a rise in the average total solar irradiance of D I = 1.65 ± 0.23 Wm-2.
The coronal source flux
The coronal source surface is where the solar magnetic field becomes approximately radial and lies at a heliocentric distance of about 2.5 solar radii [Wang and Sheeley, 1995]. The total magnetic flux leaving the sun, and thereby entering the heliosphere by threading this surface, is the coronal source flux, Fs. Lockwood et al. [1999] have developed a method for estimating annual means of the magnitude of the interplanetary magnetic field, Bsw, from the aa geomagnetic index [Mayaud, 1972]. This exploits two strong and extremely significant correlations between the IMF, the solar wind and the aa index [Stamper et al., 1999; Lockwood et al., 1999]. The annual means of the components of the IMF at Earth are well described by Parker spiral theory [Gazis, 1996; Stamper et al., 1999] giving a correlation between Bsw and the IMF radial component, Br . The Ulysses spacecraft has shown that variations in Br with heliographic latitude are small [Balogh et al., 1995], and so the total flux threading the source surface is Fs = (|Br| ´ 4p R12)/2, where R1 = 1 AU. (The factor of a half arises because half the flux is toward the sun, half is away). In order to compute the annual means of Fs, Lockwood et al. [1999] derived the necessary exponents and coefficients from correlations between data from last three solar cycles (20-22). However, there are uncertainties concerning the calibration of the early interplanetary measurements [Gazis, 1996], particularly for the solar wind concentration, Nsw. Consequently, a slightly different approach has been adopted here. All the exponents and coefficients have been derived using data from cycles 21 and 22 only. The predictions for cycle 20 have then been compared with the IMF observations. Thus the cycle 20 IMF data provide a fully independent test of the method.
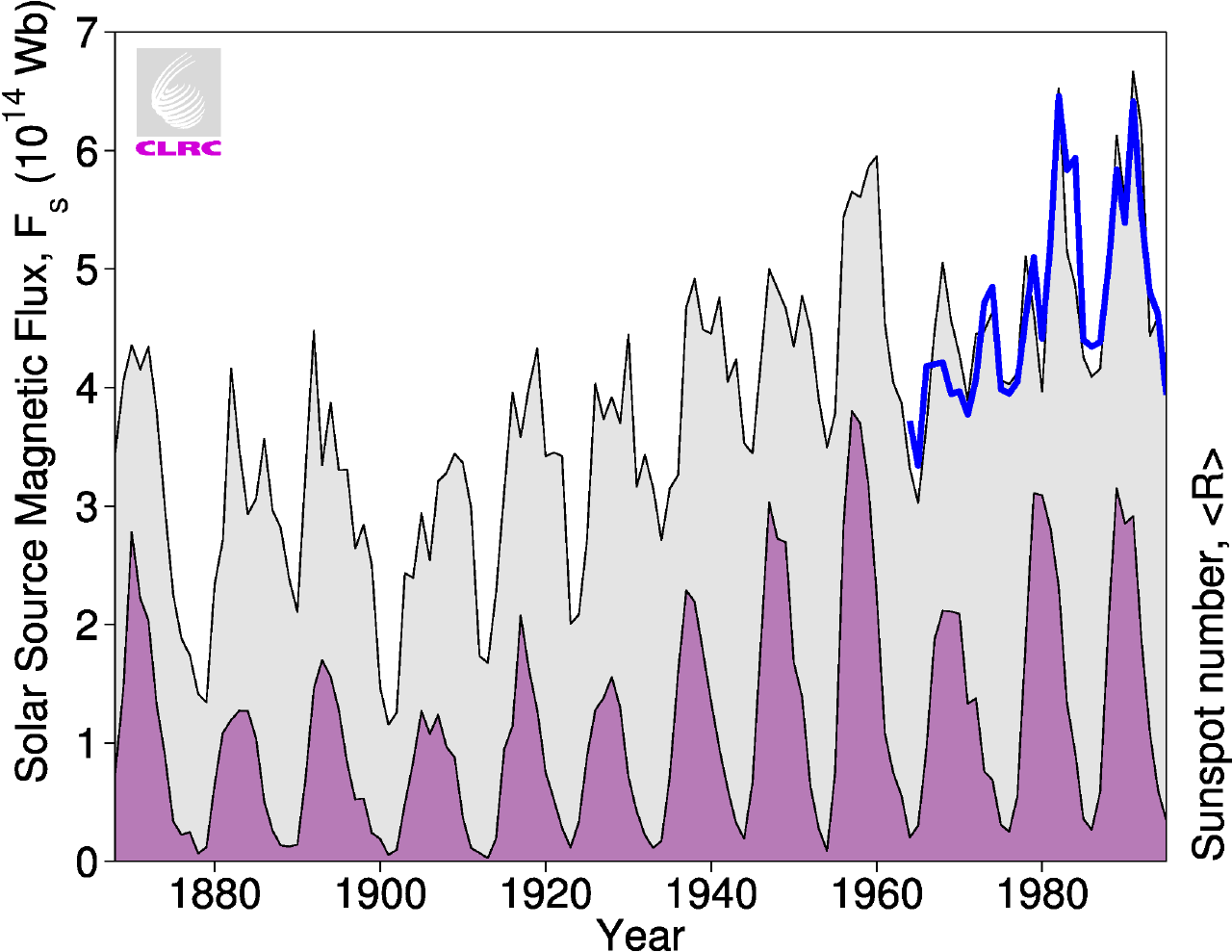
Figure 1. shows the variation of coronal source flux between 1868 and 1995, derived in this way from the aa index (Fs, shaded grey). The solid line shows the value Fso that is derived for the last three solar cycles from the annual means of the observed radial IMF component, Br. The darker-shaded region shows the sunspot number variation for comparison. Table 1 shows the RMS deviation of Fs from Fso is similar for all three cycles (respectively, 12%, 11% and 10% of <Fso> for cycles 20, 21 and 22). Thus the method has reproduced the variation in annual means well, despite the fact that cycle 20 is unusual and different from cycles 21 and 22 in many ways. Table 1 also gives the minimum-to-minimum averages, <Fs> and <Fso>, for each sunspot cycle. It can be seen that the error e m in <Fs> is only 1.5% for the test data, rather better than the 4.5% for cycle 21, one of the fitted cycles. (Note that the largest contributor to these small uncertainties is invariably the correlation between Bsw and Br). Thus the method has successfully extrapolated from cycles 21 and 22 to cycle 20. This means we can apply the method to all the aa data, back to 1868, with considerable confidence. Note that Figure 1 is not significantly different from the results of Lockwood et al. [1999] who used correlations based on data from all three solar cycles.
Figure 1 shows that Fs peaks shortly after the maximum of each sunspot cycle, at about the time that the polarity of the solar field flips. In addition to the solar cycle variation, there has been a persistent rise in Fs since the turn of the century. The rise is by a factor of 41% since 1964 and 131% since 1901 [Lockwood et al., 1999]. We note that the rise in recent cycles can also be seen in the Fso and Br data [Stamper et al., 1999] and in the results of Wang and Sheeley [1995], who mapped the observed photospheric field to the coronal source surface and 1AU using an improved allowance for magnetograph saturation effects.
Table 1. Comparison of Fso observed from IMF and Fs estimated using the aa index for solar cycles 20, 21 and 22
|
Solar Cycle Number |
Fitted or test data? |
<Fso> (1014 Wb) |
<Fs> (1014 Wb) |
<Fso> - <Fs> (1014 Wb) |
% error, e m = (100/<Fso>) ´ |<Fso> - <Fs>| |
<(Fso -Fs)2>1/2 (1014 Wb) |
% error, e = 100/<Fso>) ´ <(Fso -Fs)2>1/2 |
|---|---|---|---|---|---|---|---|
|
20 |
Test |
4.0881 |
4.0253 |
0.0628 |
1.54 |
0.4930 |
12.1 |
|
21 |
Fitted |
4.9555 |
4.7316 |
0.2239 |
4.52 |
0.5527 |
11.2 |
|
22 |
Fitted |
5.0685 |
5.1087 |
-0.0402 |
0.79 |
0.4855 |
9.6 |
Total Solar Irradiance
The output of the sun has been monitored since 1980 by a variety of instruments, specifically: the Earth Radiation Budget (ERB) instrument on the Nimbus spacecraft; the Active Cavity Radiometer Irradiance Monitor (ACRIM1) on Solar Maximum Mission (SMM); the Earth Radiation Budget Satellite (ERBS); and ACRIM2 on the Upper Atmosphere Research Satellite (UARS). Of these, the two ACRIM experiments have been able to monitor the degradation of their own sensors, which occurs most rapidly early in the lifetime of the instruments. These observations show there is a solar cycle variation in the total solar irradiance, I, of about 0.1%, but the different instruments give different absolute values of I because they are not consistently calibrated [see Willson, 1995]. There are two contributions to the solar cycle variation of I: sunspots are cooler darker regions of the photosphere, but their effects are outweighed by associated brightenings like faculae [Lean et al., 1995]. Both sunspot darkening and facular brightening are magnetic phenomena. If the variation in Fs reflects changes in the solar dynamo, we would expect associated changes in the surface field in regions of closed flux where sunspots and faculae form. Thus we might expect some relationship between I and Fs.
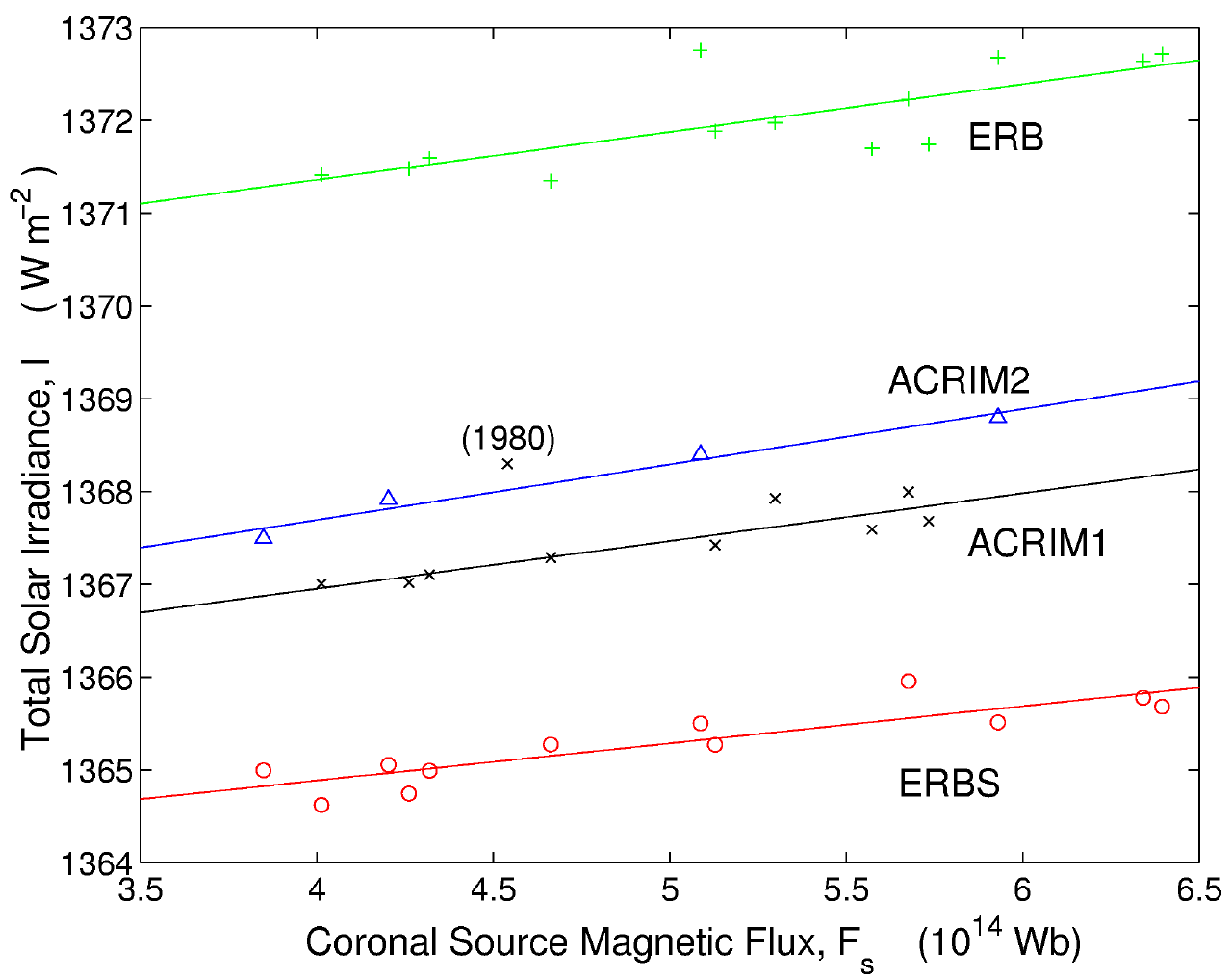
Figure 2. Scatter plots of the total solar irradiance, I, as a function of 3-year running means of annual coronal source magnetic flux values, Fs, for data from the instruments: Nimbus/ERB (+); SMM/ACRIM1 (´ ); UARS/ACRIM2 (D ); and ERBS (o). The lines are linear regression fits to each data set.
Figure 2 shows annual means of the total solar irradiance measured by the four instruments as a function of the simultaneous Fs, as deduced from the aa index data. To eliminate some shorter period fluctuations, we use 3-year running means of the annual Fs values. In each case, there is clear dependence but the difference in the sensitivity and offset of each instrument is apparent. Least-squares linear fits for each data set are also shown in Figure 2: the slope s, intercept (at Fs = 0) c, correlation coefficient r, and significance level of each fit are given in Table 2. The worst agreement is for the early data points, for 1979 and 1980. In the case of the ERB data, this is likely to be due, at least in part, to the rapid early degradation of the sensors and these data have been omitted. However, higher-than-expected I is also seen by ACRIM2 in 1980 (the point labelled in Figure 2). This is also true for the reconstructed I produced by Lean et al. [1995]. Because it was obtained by a self-monitoring instrument, this data point has been included in the present study; however, its inclusion was found not to introduce any significant change to the regressions values derived.
Table 2. Regression fits between total solar irradiance, I, and coronal source flux Fs ( I = s´ Fs+ c)
|
TSI Monitor |
Years (inclusive) |
slope, s (10-14Wm-2Wb-1) |
intercept, c (Wm-2) |
correlation coefficient, r |
Significance (%) |
|
Nimbus/ERB |
1981-1993 |
sN = 0.5159 |
1369.3 |
0.7564 |
100-0.139 |
|
SMM/ACRIM1 |
1980-1989 |
sA1 = 0.5142 |
1364.9 |
0.9067 |
100-0.037 |
|
ERBS |
1984-1995 |
sE = 0.4010 |
1363.3 |
0.8798 |
100-0.008 |
|
UARS/ACRIM2 |
1992-1995 |
sA2 = 0.5978 |
1365.3 |
0.9861 |
100-0.693 |
|
All |
1981-1995 |
<s>± s s = 0.507± 0.070 |
1364.9 |
0.8516 |
100-6.15´ 10-10 |
|
All |
1981-1995 |
smax = <s>+s s = 0.577 |
1364.6 |
0.8516 |
100-6.15´ 10-10 |
|
All |
1981-1995 |
smin = <s>-s s = 0.437 |
1365.3 |
0.8516 |
100-6.15´ 10-10 |
The key parameter for extrapolation of I to earlier times is the slope of the regression line s. The average s from the four instruments, <s>, is taken to have an error of its standard deviation ss, giving a possible range of values between smin = <s> - s s and smax = <s> + ss. The ACRIM2 and the ERBS values lie close to, but just outside, this range. Given that the instrumental accuracy of ACRIM2 should be the highest of the four instruments, the best estimate of the slope may well be nearer smax than <s>. The ACRIM2 data also give the highest correlation coefficient; however, because this data sequence is relatively short, this correlation has the lowest statistical significance (which, nevertheless, exceeds 99%). For each of the instruments, neither the systematic offset nor the sensitivity is accurately known. We here combine the data from the different instruments by adopting a value for s and then evaluating a mean c for this s and hence the systematic offsets for each instrument. This was done for slopes of smin , <s> and smax; the results for the average slope <s> are shown in Figure 3. Table 3 gives the offset, d, and sensitivity ratio, g, for our inter-calibration of the various solar output monitors. Values are broadly consistent with the ratios obtained by Willson [1995].
The solid line in Figure 3 is the regression to the full dataset, inter-calibrated in this way. The correlation coefficient for the combined data is given in Table 2 and is comparable to those for the individual datasets; however, the significance level is higher because of the greater number of samples. We note that this correlation between Fs and I offers an explanation of the link between the aa index and global surface temperature on Earth [Cliver et al., 1998].
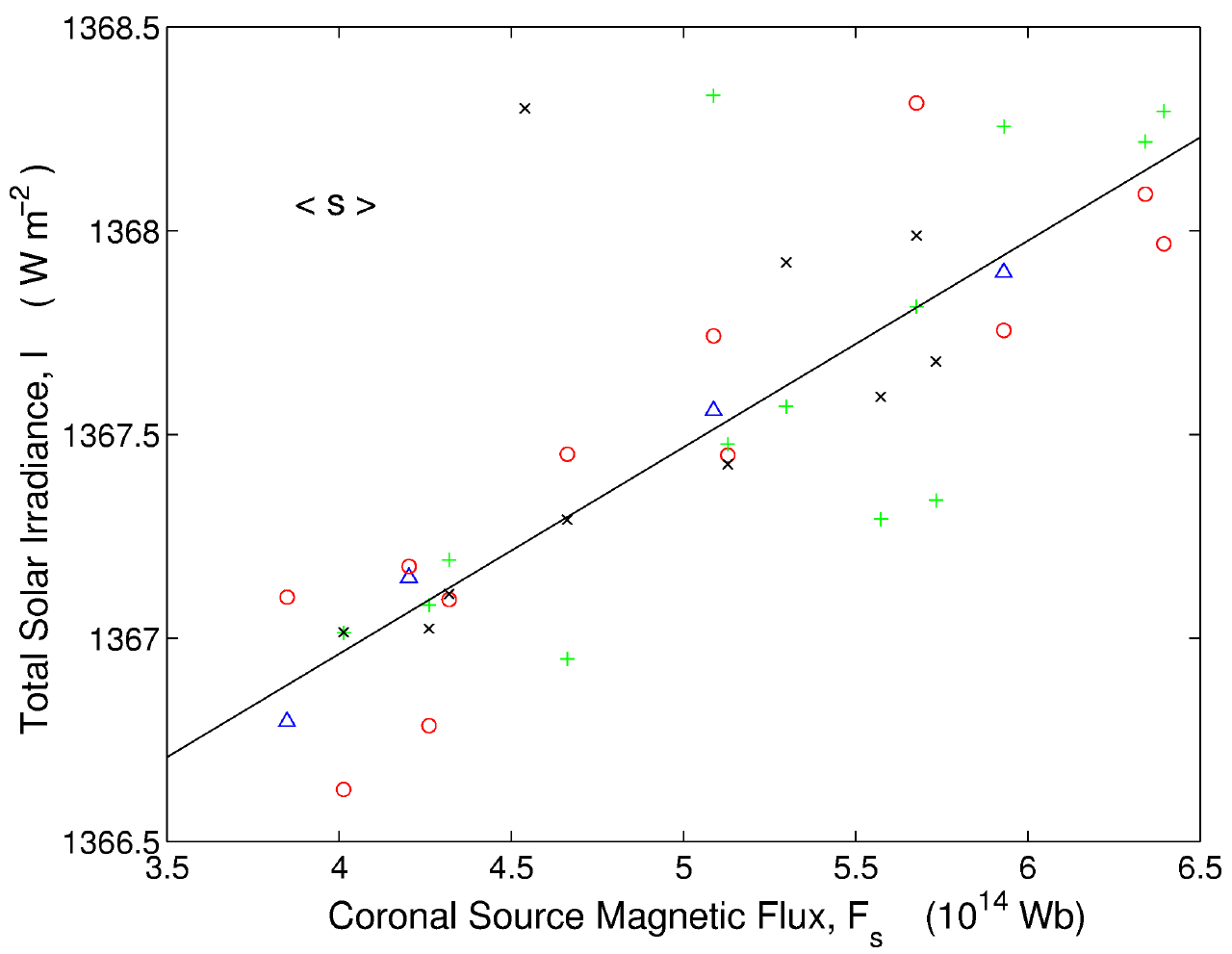
Figure 3. Same as figure 2, with data inter-calibrated using the average slope <s> of the regression lines (see Table 3).
Table 3. Calibration of total solar irradiance I for the observed values Io from the various solar monitors,
where (I -1365) = g(Io -1365) + d and both I and Io are in units of W m-2
|
TSI Monitor |
<s> |
smin |
smax |
|||
|
g |
d |
g |
d |
g |
d |
|
|
Nimbus/ERB |
0.9832 |
4.2934 |
0.8475 |
3.3628 |
1.1188 |
5.2240 |
|
SMM/ACRIM1 |
0.9865 |
-0.0331 |
0.8503 |
-0.3666 |
1.1226 |
0.3003 |
|
ERBS |
1.2648 |
-2.1035 |
1.0903 |
-2.1512 |
1.4394 |
-2.0557 |
|
UARS/ACRIM2 |
0.8485 |
0.3260 |
0.7314 |
-0.0570 |
0.9656 |
0.7091 |
Long-term drift in total solar irradiance
We assume that the relation between I and Fs, as revealed using data from solar cycles 21 and 22 in the previous section, is valid at all times. We can then use the regressions given in Table 2 to extrapolate back to 1868. Using the mean slope for the four instruments, <s> , yields the variation shown in Figure 4. Also shown is the 11-year running mean, I11, which reveals a general upward trend. Given than the heat capacity of the oceans will smooth out most of the effects of variations in I on the timescales of the solar cycle [Wigley and Raper, 1990], these smoothed variations are most relevant to global temperature change. The form of these curves is the same for any s, but the amplitude of the solar cycle oscillations and of the long-term drift increases with s. This is illustrated by Figure 5 which shows I11 for smin , <s> and smax. Also shown in both Figures 4 and 5 are the values estimated by Lean et al. [1995]. The agreement between the forms of the two extrapolations is remarkably close, considering Lean et al used sunspot numbers to estimate sunspot darkening and facular brightening; whereas we have used an entirely independent set of measurements, namely the aa geomagnetic index. There is a tendency for Lean et al.�s values to be lower in even-numbered cycles, particularly early in the century. For slopes smin <s> and smax, we find that the average total solar irradiance I11 increased by DI = 1.65 ± 0.23 Wm-2 in the interval 1901-1995, up to the value of 1367.6 Wm-2 . The lowest value of this range (D I = 1.420 Wm-2) is a 0.10% change, whereas the largest (D I = 1.875 Wm-2) is a 0.14% change. Lean et al. derived a slightly larger change of D I = 2.106 Wm-2 over the same interval. The most precise instrument, ACRIM2, gives a slope sA2 that is close to smax, and thus the estimate by Lean et al. for the magnitude in the upward drift in I is in close agreement with the most likely value found here.
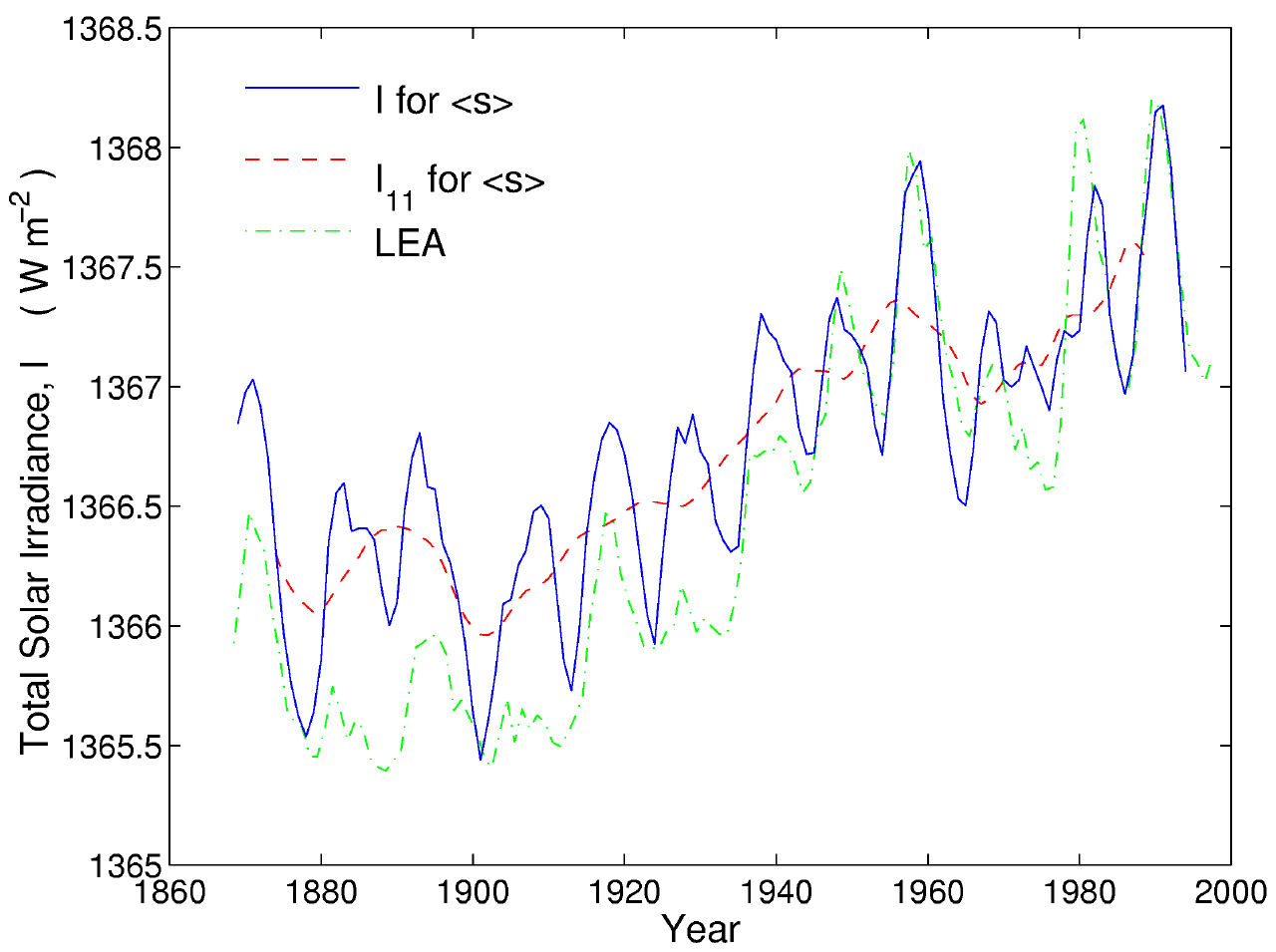
Figure 4. The variation of the inferred total solar irradiance I (solid line) and its 11-year running mean I11 (dashed line), deduced using the mean of the regression slopes, <s>. The dot-dash line is from Lean et al. [1995].
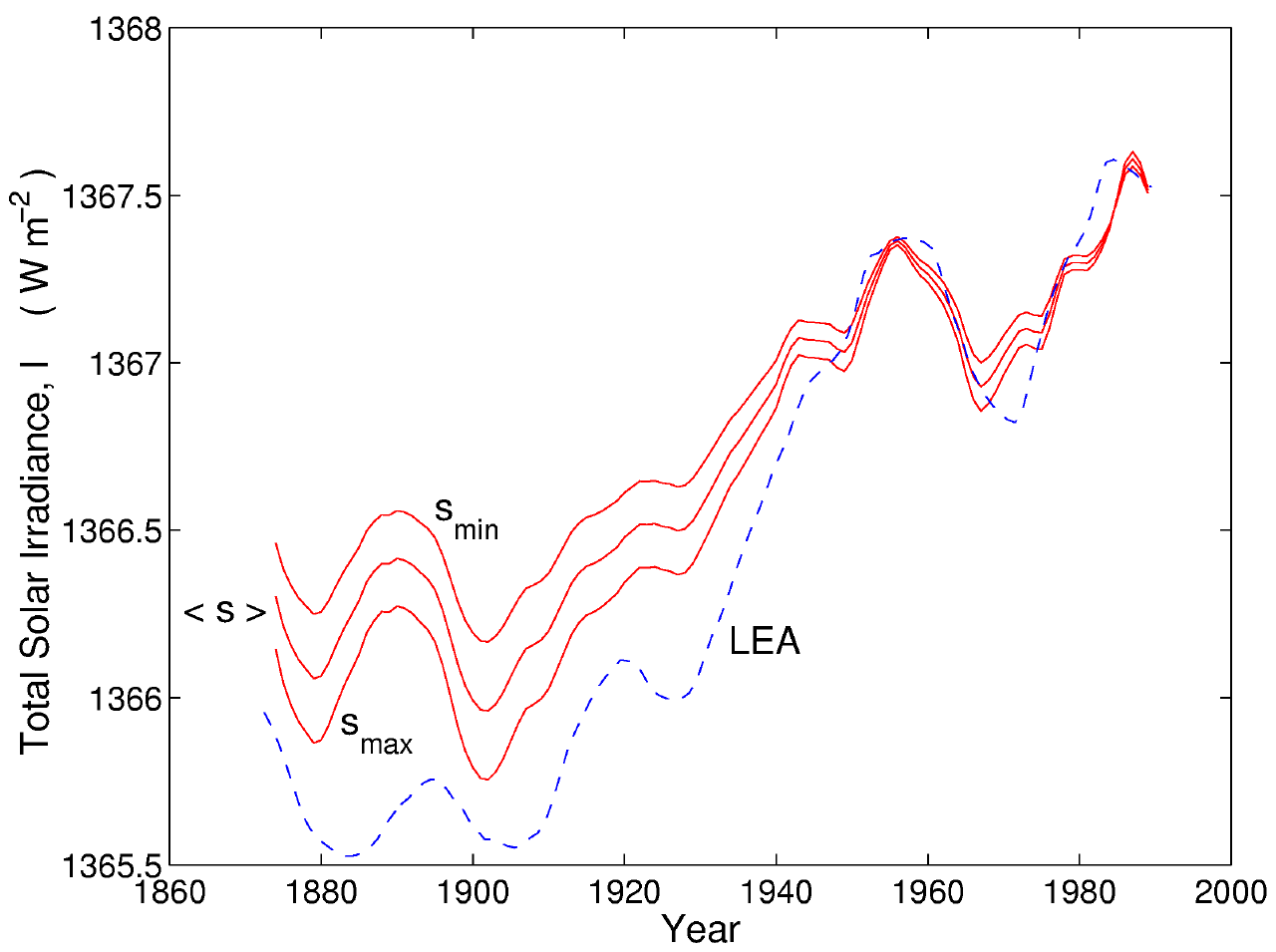
Figure 5. The variations of the 11-year running means of the inferred total solar irradiance I11, for the minimum, mean and maximum regression slopes smin , <s> and smax. The dashed curve labelled LEA is from Lean et al. [1995].
The mean rise in Fs (and Fso) over last three solar cycles is at a rate of 0.5 ´ 1014 Wb per decade and using smin , <s> and smax from our regression analysis gives a rate of increase in I of 0.25± 0.4 Wm-2 per decade. We can compare this range with the estimates made from inter-calibrated measurements during the minima at the start of cycles 22 and 23 by Willson [1995]. He reported 0.50 and 0.37 Wm-2 per decade for ACRIM1/2 and ERBS, respectively. Thus our estimates of the recent of rise in I are comparable with, but somewhat smaller than, those by Willson.
The rise in I reported here D I is significant, giving a rise in the radiative forcing at the top of the atmosphere of D Q = D I(1-a)/4 » 0.29± 0.04 Wm-2, where a is the Earth�s albedo. This is comparable with the 0.3 Wm-2 estimated by the Intergovernmental Panel on Climate Change (IPCC) for the same interval [Schimel et al., 1996]. Given that the IPCC estimate that the effect of anthropogenic greenhouse CO2 is equivalent to 1.5 Wm-2, the change in I shown in Figure 5 implies a significant role for solar forcing of terrestrial climate change, as has also been suggested by a number of other recent studies [e.g. Lean et al., 1995; Cliver et al., 1998]. The effect on global mean surface temperatures will be complex because the change in I will be made up of contributions that are much stronger at some wavelengths (for example UV) than at others and because a variety of other effects (for example, changes in anthropogenic greenhouse gases, tropospheric sulphate aerosols and volcanic dust in the stratosphere) will also be active and will interact with each other in complex feedback loops [Rind and Overpeck, 1993]. We use the simple relationship D Ti = -200.59 + 0.1466´ I , where D Ti is the inferred temperature change (in ° C) relative to the mean observed value during solar cycle 11 [from Lean et al., 1995 and Rind and Overpeck, 1993], to infer rises of 0.21, 0.24 and 0.28° C for s of, respectively, smin , <s> and smax. This should be compared to a rise in the global mean observed temperature D To of 0.66 ° C over the same interval [Parker et al., 1994]. The net trend in D To over the period 1870-1910 is not significantly inconsistent with the variation of the inferred solar output. On the other hand, the change in solar luminosity can account for only 52% of the rise in D To over the period 1910-1960 but just 31% of the rapid rise in D To over 1970-present. In the interval covered by Figure 5, CO2 in the atmosphere increased from 280 to 355 ppmv. The implications are that that the onset of a man-made contribution to global warming was disguised by the rise in the solar constant and that the anthropogenic effect may have a later, but steeper, onset. This delay may have been due to an increase in the albedo a caused by aerosols or to reduced radiative forcing D Q due to ozone depletion. There is other evidence to support this view of the role of solar forcing: for example, the decrease in global temperatures during about 1950-1965 was at a time when the concentration of greenhouse gasses was increasing [Friis-Christensen and Lassen, 1991] and the inferred decrease in solar luminosity may help explain this. Furthermore, the present upward trend in global temperatures commenced before significant burning of fossil fuels [Bradley and Jones, 1993] and there is some evidence that temperatures have been as high in past epochs as they are now [see Cliver et al., 1998]. Recently, Tett et al. [1999] have used a set of simulations made by a coupled atmosphere-ocean global circulation model to deduce a shift from solar forcing to anthropogenic effects as this century has progressed.
Acknowledgements This work made use of databases and systems of the World Data Centre WDC-C1 at RAL. We thank M. Wild who is responsible for the WDC facility and the UK Particle Physics and Astronomy Research Council who have funded both this research and the facility. We thank Dr Judith Lean for the Lean et al. TSI reconstruction data and the many scientists who have contributed data to the WDC system.
References
Balogh, A., E.J. Smith, B.T. Tsurutani, D.J. Southwood, R.J. Forsyth and T.S. Horbury, The heliospheric field over the south polar region of the sun, Science, 268, 1007-1010, 1995.
Bradley, R.S. and P.D. Jones, "Little Ice Age" summer temperature variations: their nature and relevance to recent global warming trends, The Holocene 3(4), 367-376, 1993.
Cliver, E., V. Boriakoff, and K.H. Bounar, Geomagnetic activity and the solar wind during the Maunder minimum, Geophys. Res. Lett., 25, 897-900, 1998.
Friis-Christensen, E. and K. Lassen, Length of the solar cycle: an indicator of solar activity closely associated with climate, Science, 245, 698-700, 1991.
Gazis, P.R., Solar cycle variation of the heliosphere, Rev. Geophys., 34, 379-402, 1996.
Lean, J., J. Beer, and R. Bradley, Reconstruction of solar irradiance since 1610: implications for climate change, Geophys. Res. Lett., 22, 3195-3198, 1995.
Lockwood, M., R. Stamper, and M.N. Wild, A Doubling of the Suns� Coronal Magnetic Field during the Last 100 years, Nature in press, 1999.
Mayaud, P.N., The aa indices: a 100-year series characterising the magnetic activity, J. Geophys. Res., 72, 6870-6874, 1972.
Parker, D.E., P.D. Jones, A. Bevan, and C.K. Folland, Interdecadal changes of surface temperatures since the late 19th century, J. Geophys. Res., 99, 14373-14399, 1994.
Rind, D. and J. Overpeck, Hypothesized causes of decade-to-decade climate variability: climate model results, Quaternary Sci. Rev., 12, 357-374, 1993.
Schimel, D., et al., Radiative forcing of climate change, in "Climate Change, 1995: The Science of Climate Change", Chapter 2, Cambridge University Press, 1996.
Stamper, R., M. Lockwood, M.N. Wild, and T.D.G. Clark, Solar Causes of the Long-Term Increase in Geomagnetic Activity, J. Geophys Res. Submitted, 1999.
Tett, S., P.A. Stott, M.R. Allen, W.J. Ingram and J.F.B. Mitchell, Causes of twentieth century temperature change, Nature, in press, 1999.
Wang, Y.-M. and N.R. Sheeley, Jr., Solar implications of Ulysses interplanetary field measurements, Astrophys. J., 447, L143-L146, 1995.
Wigley, T.M.L. and S.C.B. Raper, Climatic change due to solar irradiance changes, Geophys. Res. Lett., 17, 2169-2172, 1990.
Willson, R.C., Total solar irradiance trend during cycles 21 and 22, Science, 277, 1963-1965, 1997.
_____
M. Lockwood and R. Stamper, RAL, Chilton, Didcot, Oxfordshire, OX11 0QX, England, UK. (e-mail: m.lockwood@rl.ac.uk)
(Received May 10, 1999,
accepted May 28, 1999)
1 Also at Southampton University, Southampton, UK
Copyright 1999 by the American Geophysical Union.